TheRealTMA
Senior Member
- Joined
- Jul 13, 2012
- Posts
- 8,223
- Qantas
- Platinum
Thought so. Stayed in Petersham Hotel on way to Spain in September '17. Pics from hotel. (Went to Petersham Nursery for lunch with friends!)
View attachment 262617View attachment 262618
View attachment 262619

Ah well. Would not have known that one!I was going to post this if an extra clue was required...
View attachment 262620
Is the dining experience up to the hype? If it was 2017 - did that mean Skye Gyngell was chef?Thought so. Stayed in Petersham Hotel on way to Spain in September '17. Pics from hotel. (Went to Petersham Nursery for lunch with friends!)
View attachment 262617View attachment 262618
View attachment 262619
AFF Supporters can remove this and all advertisements
Food was excellent! I think she had left for Somerset House by then?Is the dining experience up to the hype? If it was 2017 - did that mean Skye Gyngell was chef?
Thanks …and for the photos - enjoyed looking at that menu #bucketlist! Plan on being in London again next year - I can’t believe I just wrote thatFood was excellent! I think she had left for Somerset House by then?
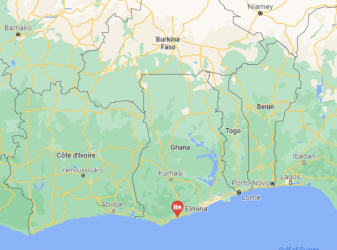

I hope to get to Ghana in a year or two. Thanks for sharing.No takers. On the left is Elmina Castle on the south-western coast of Ghana, built in the 1400s and the oldest building south of the sahara. It was a slave fort. I was in Ghana on business in about 1998 and when finished hired a car and cruised around the south of the country. Can't really believe I did that!
View attachment 262669
Looking the other way
View attachment 262668
Argentina. Needs a steam loco on it to really complete the picture. "Railway to the Heavens" if memory serves me right. I never got to see that, but rode steam further south from Esquel to El Maiten in the 80s. Beautiful bridge in the harsh desert. Lovely shot.Where am I?
Argentina. Needs a steam loco on it to really complete the picture. "Railway to the Heavens" if memory serves me right. I never got to see that, but rode steam further south from Esquel to El Maiten in the 80s. Beautiful bridge in the harsh desert. Lovely shot.

Is there an update or cloooo for this one?.. apologies if I was inattentive and did not see
It's on an island.Is there an update or cloooo for this one?.. apologies if I was inattentive and did not see
Sicily?It's on an island.
No and correct answer will have to include what's in the pic.Sicily?
Former capital of Corfu?No and correct answer will have to include what's in the pic.

